Free Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experience axis\(y3)^2=8(x5) directrix\(x3)^2=(y1) parabolaequationcalculator en Related Symbolab blog posts Practice Makes Perfect Learning math takes practice, lots of practice
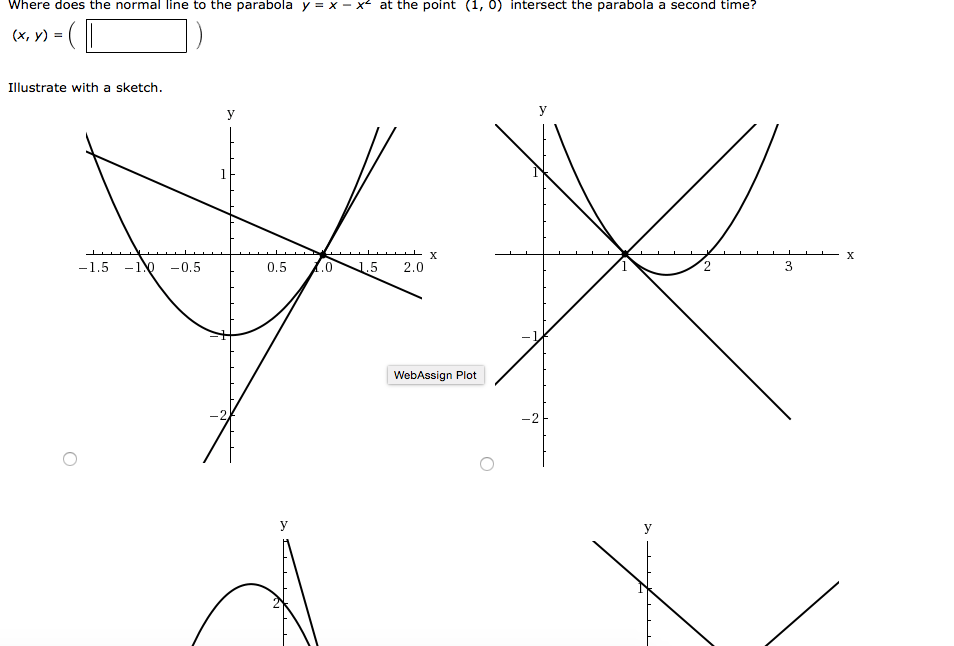
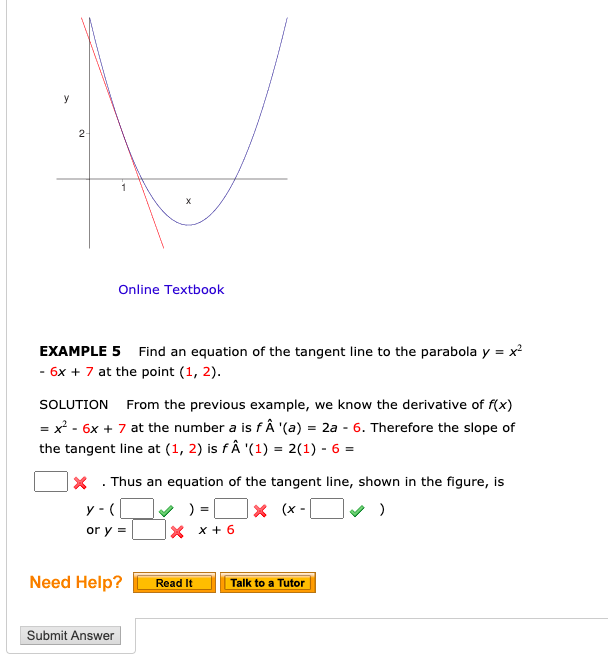
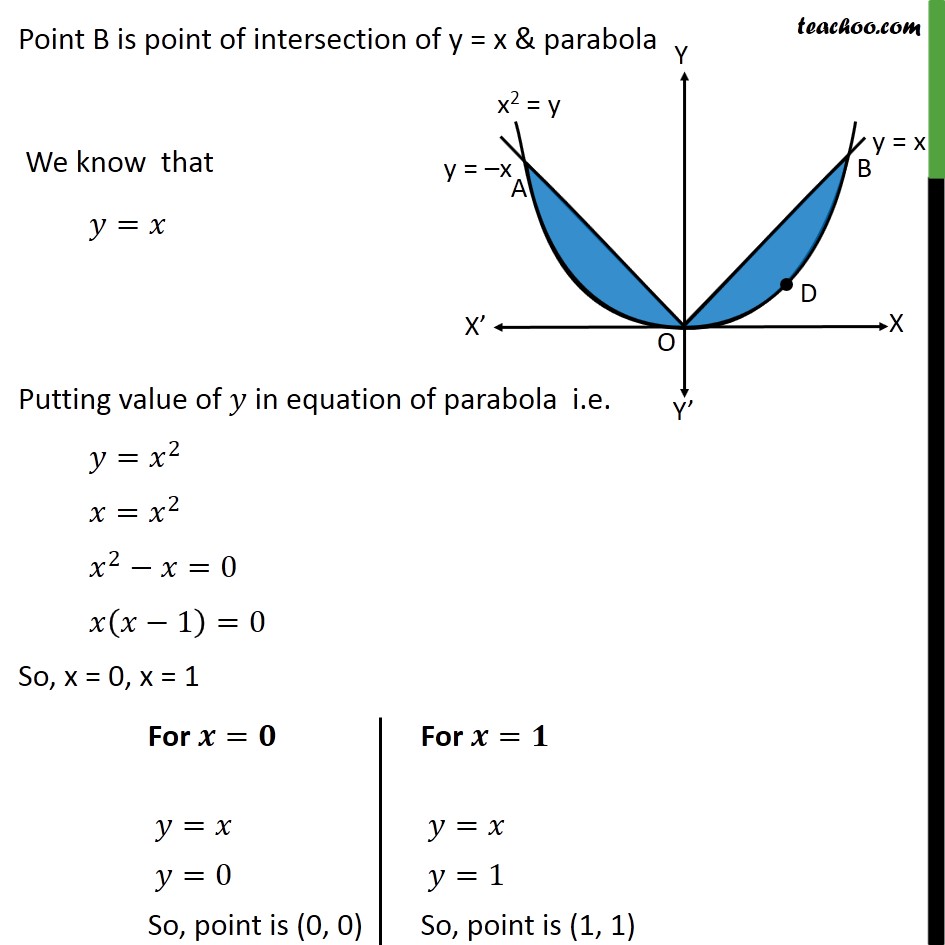
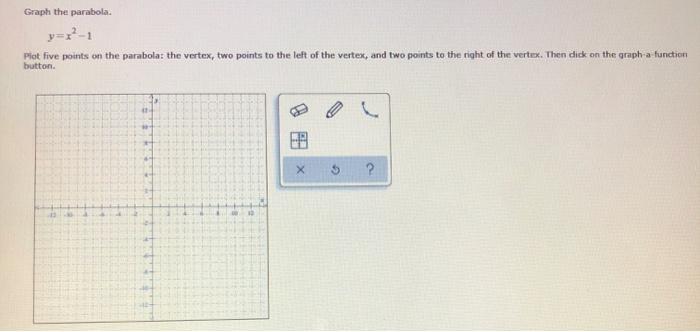
Parabola y=-x^2+2x+1-The beginning of an indepth study of graphing quadratic equations (parabolas) Includes the vocab words vertex and axis of symmetryFind all the points of intersection between the two parabolas y = x 2 3 x 1 y = x^2 3x 1 y = x 2 3 x 1 and y = − x 2 x − 1 y = x^2 x 1 y = − x 2 x − 1 We begin by equating both the expressions x 2 3 x 1 = − x 2 x − 1 2 x 2 2 x 2 = 0 x 2 x 1 = 0 \begin{aligned} x^2 3x 1 &= x^2 x 1 \\ 2x^2 2x 2 &= 0 \\ x^2 x 1 &= 0 \end{aligned} x 2 3 x 1 2 x 2
Parabola y=-x^2+2x+1のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  | |
 |  |  |
「Parabola y=-x^2+2x+1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | 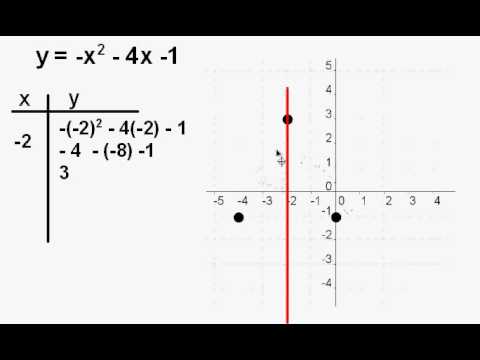 |
 |  | |
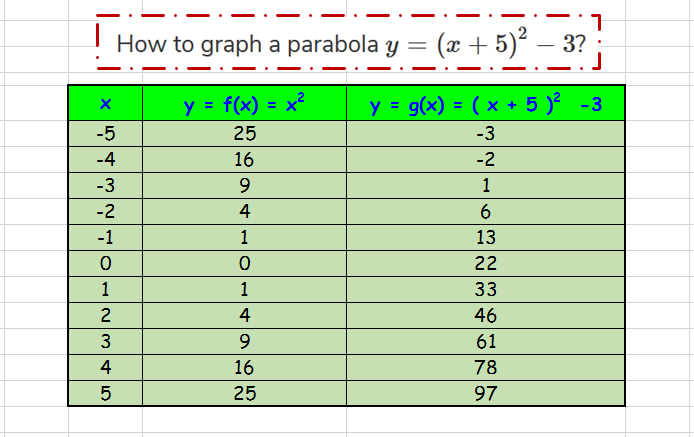 |  | |
「Parabola y=-x^2+2x+1」の画像ギャラリー、詳細は各画像をクリックしてください。
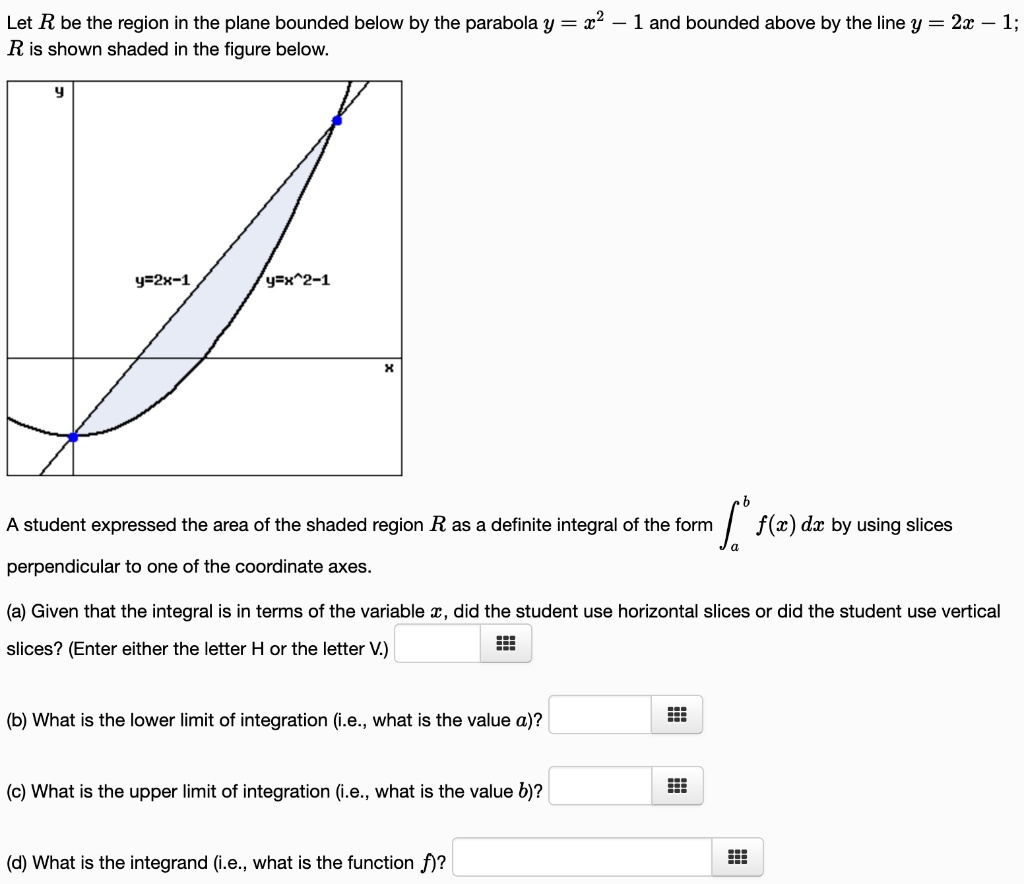 |  | 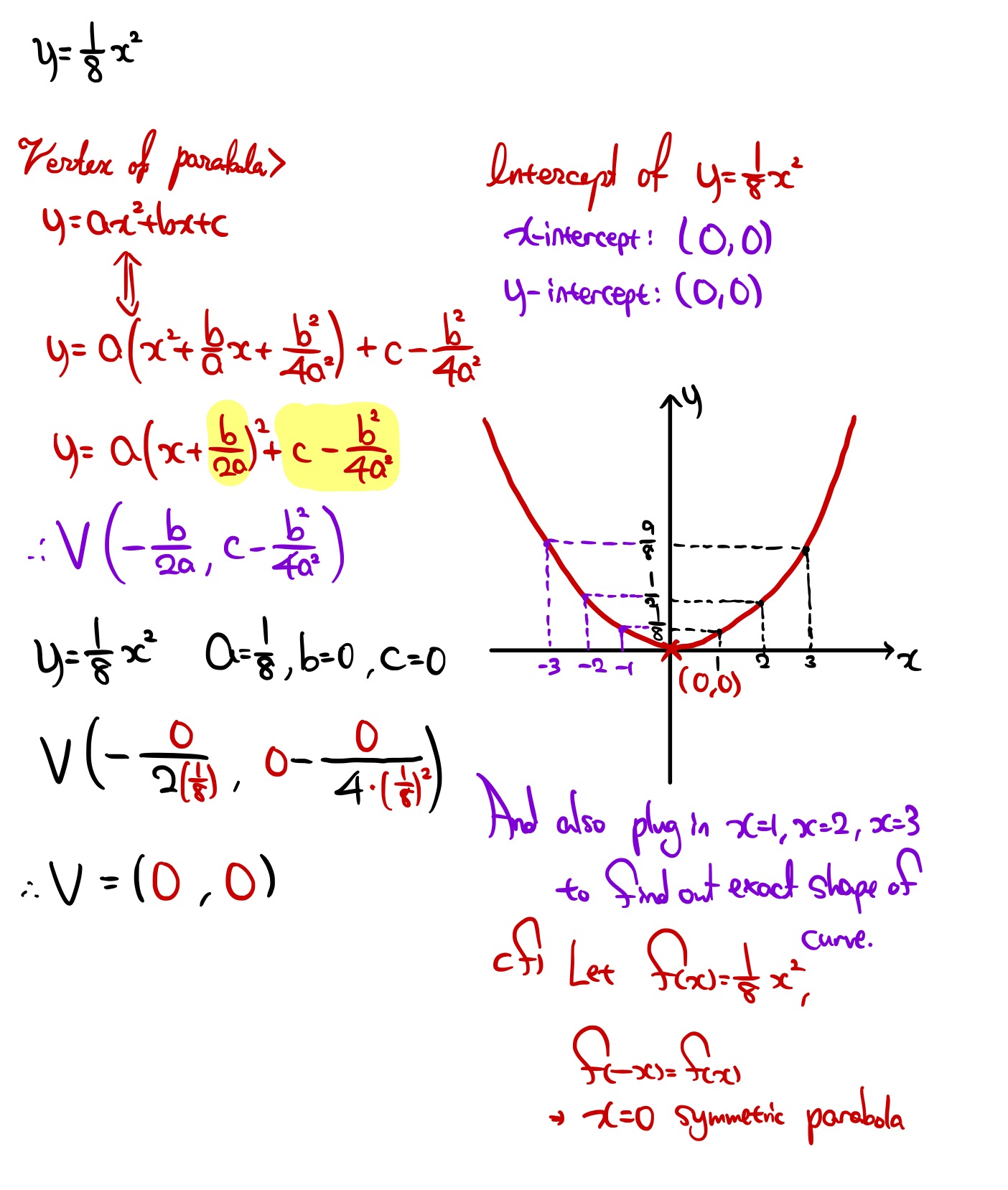 |
 |  |  |
 | ||
 |  | |
「Parabola y=-x^2+2x+1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
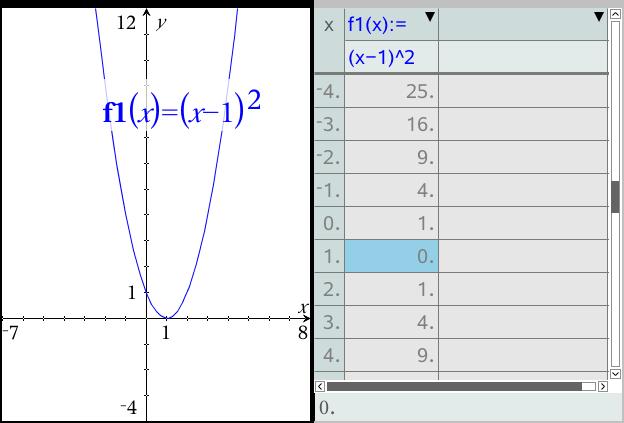 |  | |
「Parabola y=-x^2+2x+1」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 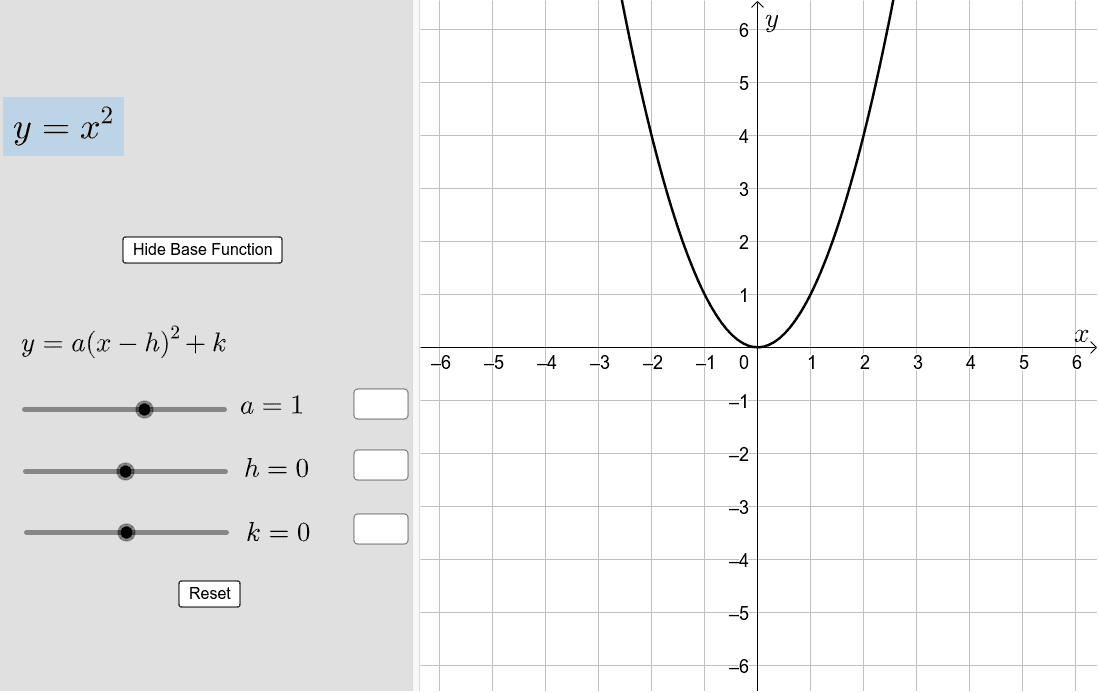 | |
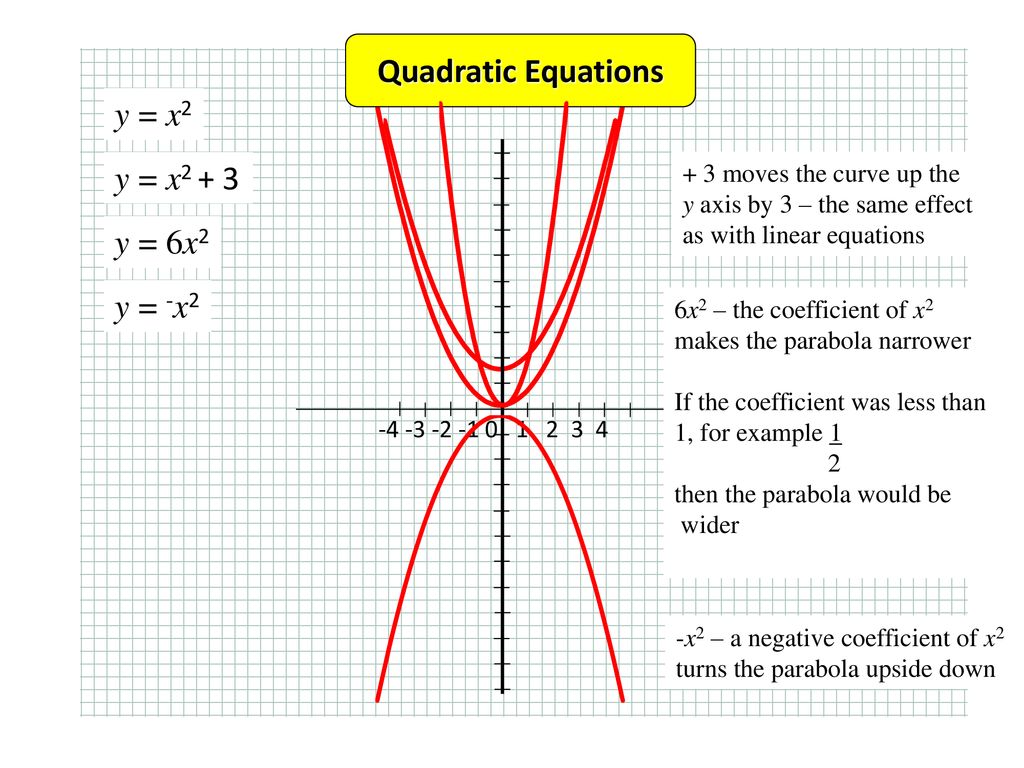 | ||
 | 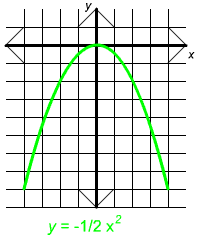 |  |
 |  |  |
「Parabola y=-x^2+2x+1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
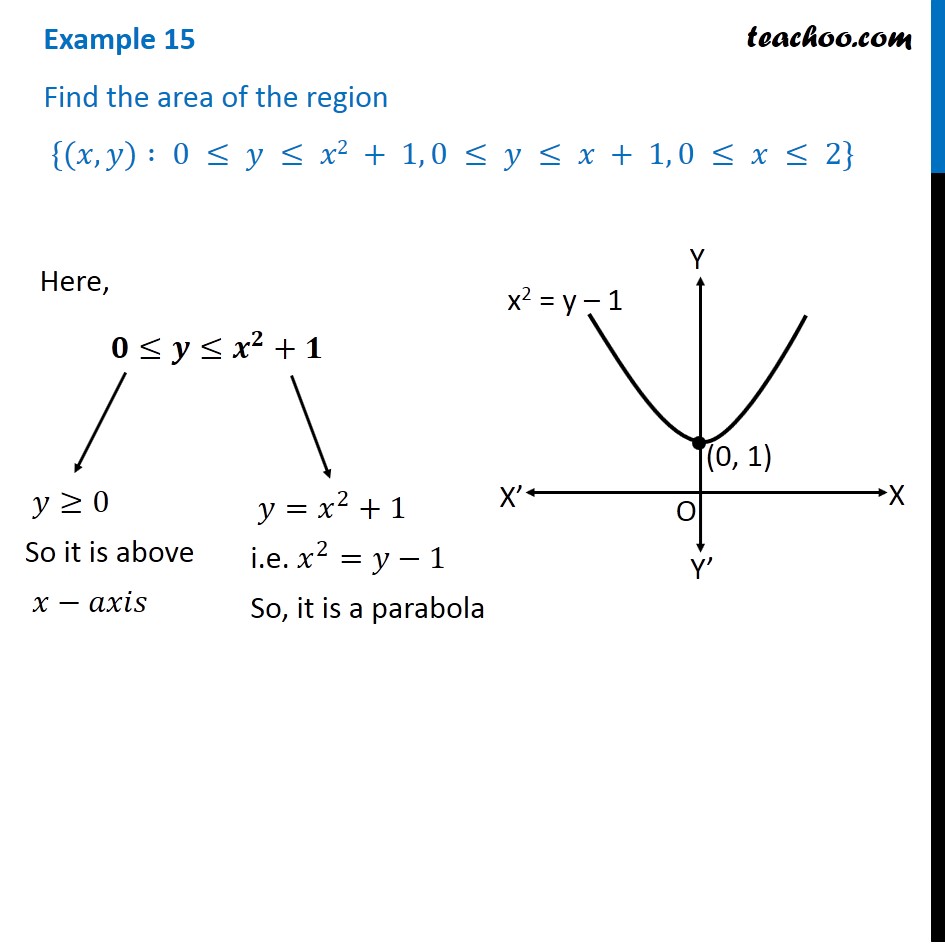 |  | |
「Parabola y=-x^2+2x+1」の画像ギャラリー、詳細は各画像をクリックしてください。
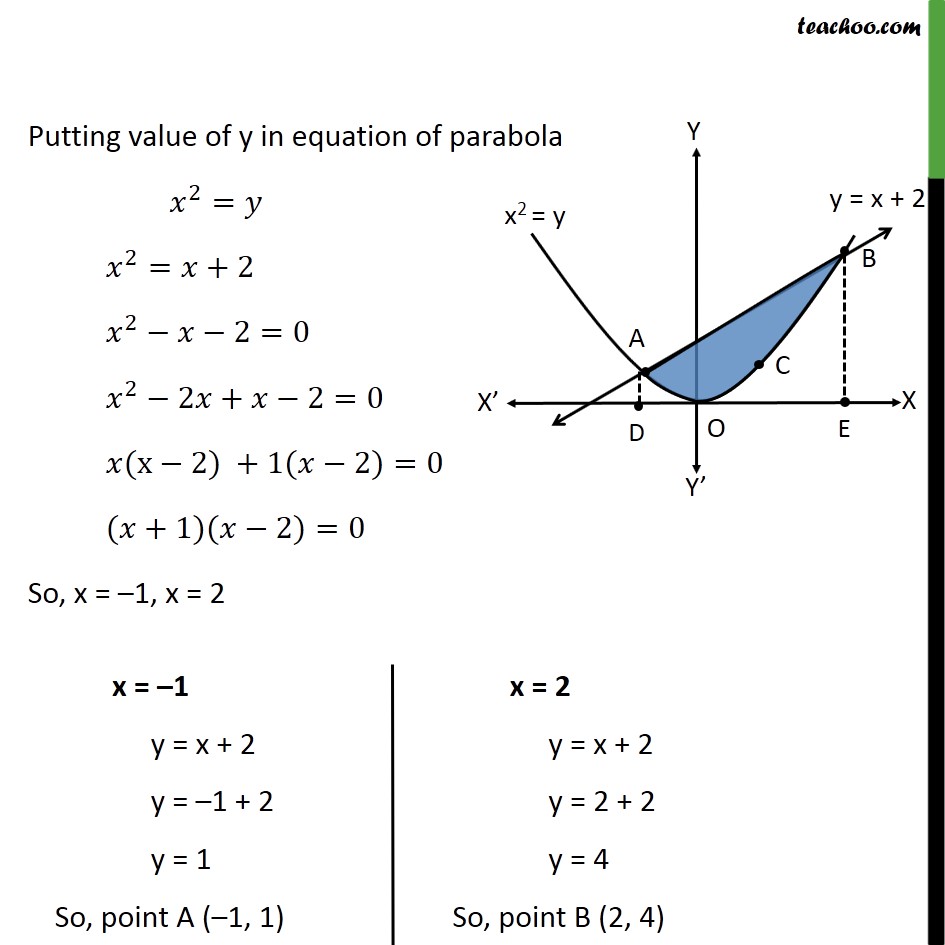 |  | |
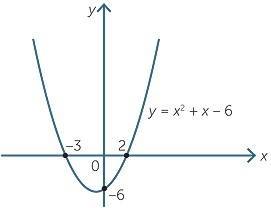 | 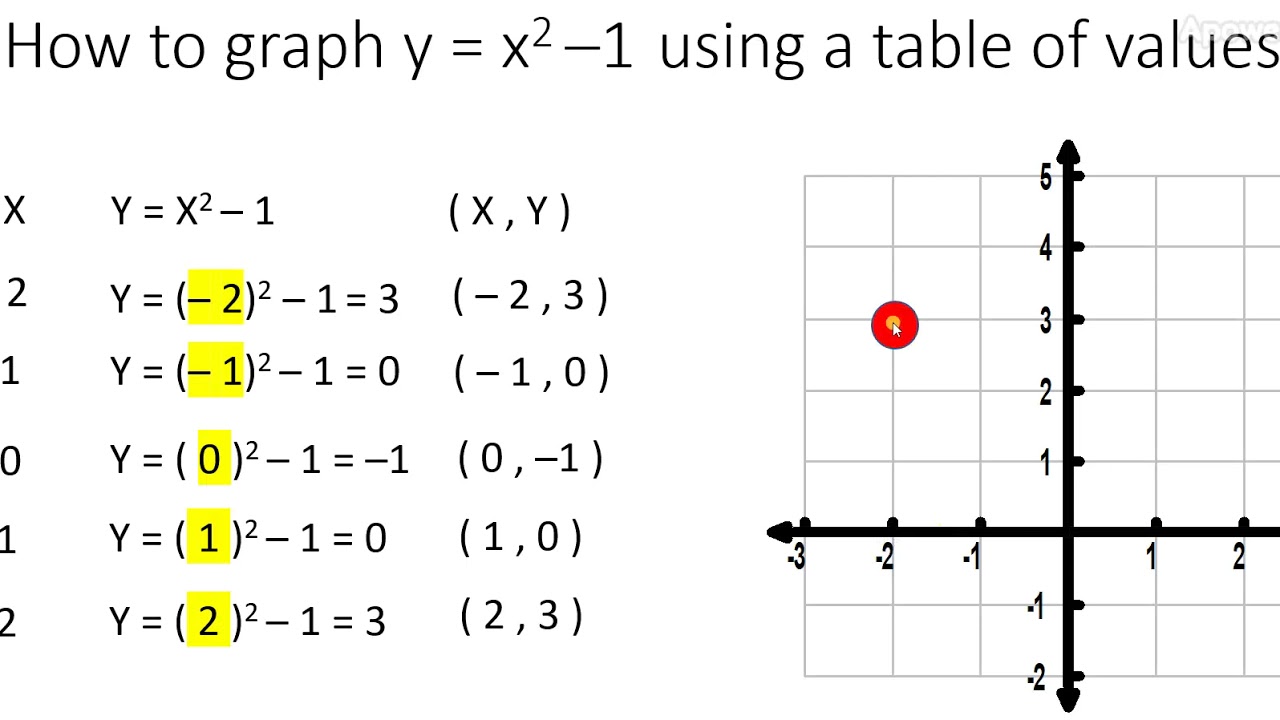 |  |
 |  | |
 |  | |
「Parabola y=-x^2+2x+1」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
 |  | |
「Parabola y=-x^2+2x+1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
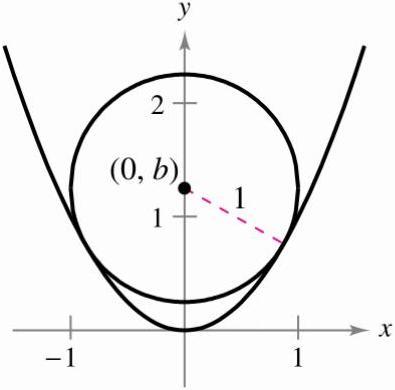
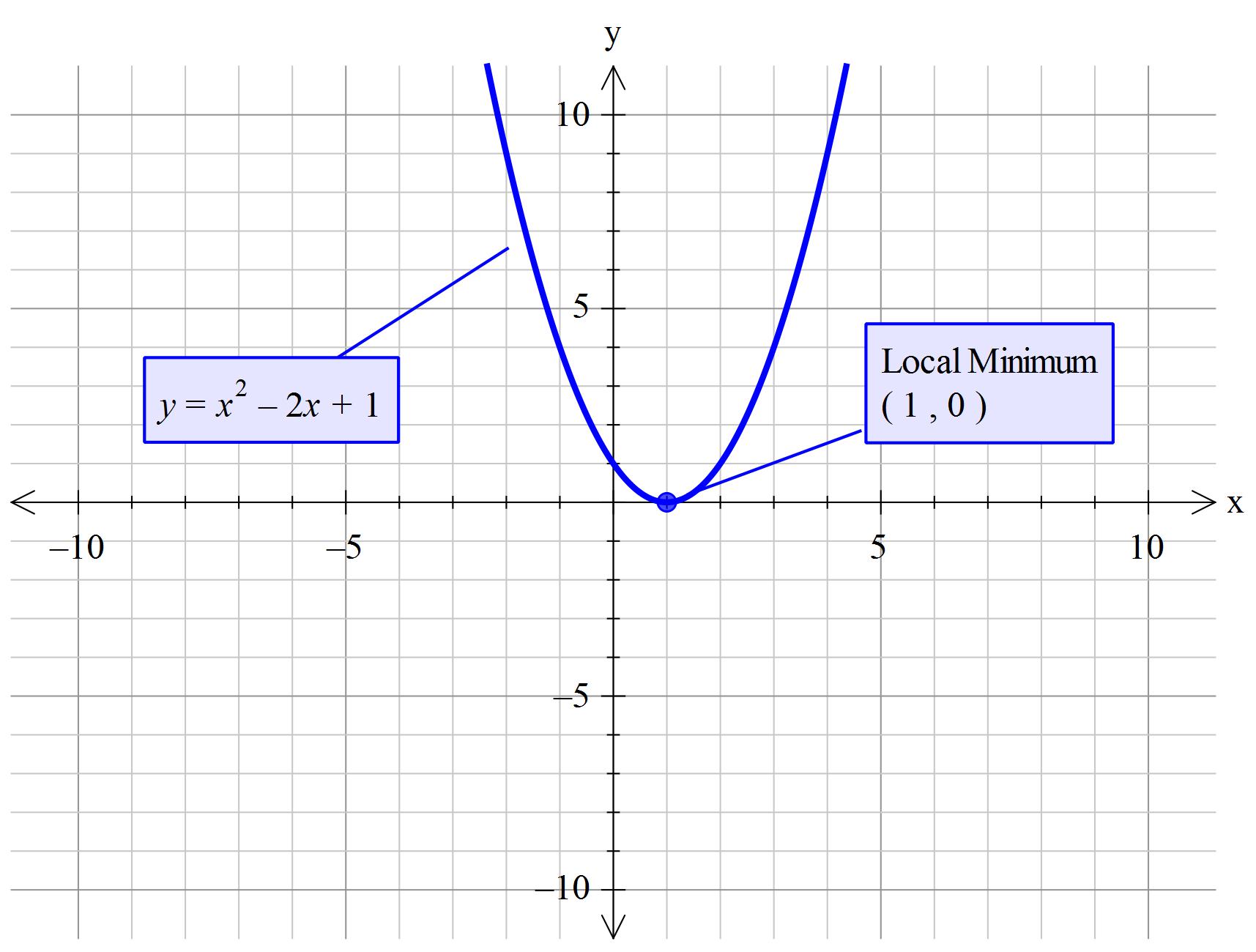
Finding the focus of a parabola given its equation If you have the equation of a parabola in vertex form y = a ( x − h) 2 k, then the vertex is at ( h, k) and the focus is ( h, k 1 4 a) Notice that here we are working with a parabola with a vertical axis of symmetry, so the x coordinate of the focus is the same as the x coordinate ofLa parabola è il luogo geometrico dei punti del piano equidistanti da un punto fisso detto fuoco e da una retta detta direttrice;
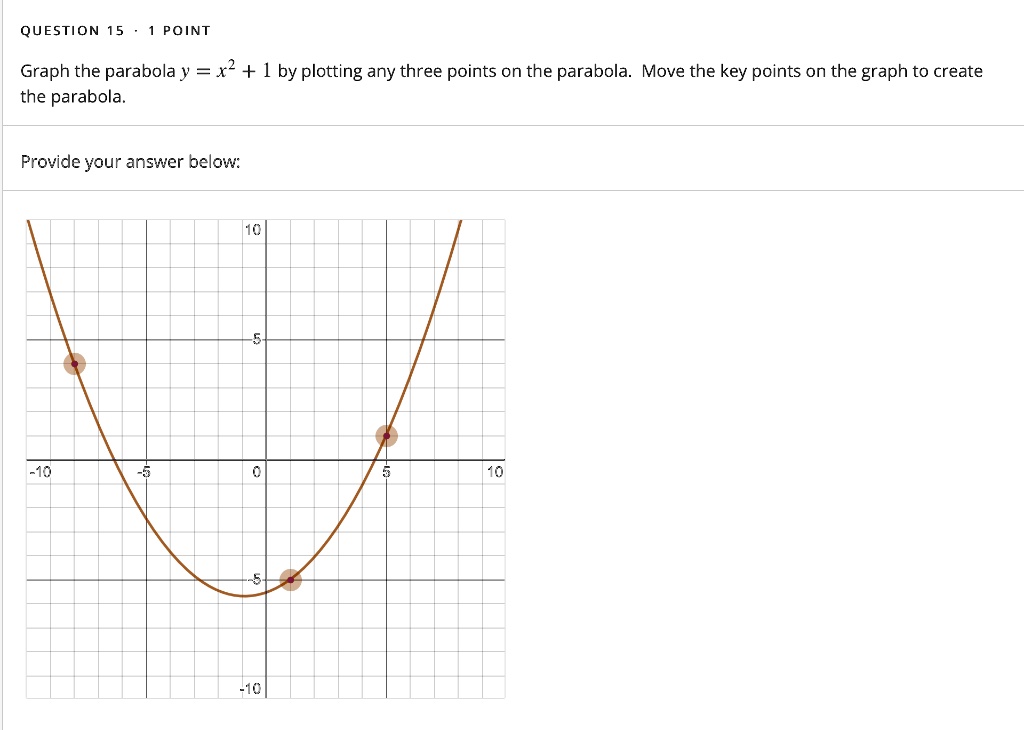
Incoming Term: parabola y=x^2+1, parabola y=x^2-16, parabola y=(x-1)^2-3, parabola y=(x-1)^2-5, grafik parabola y=x^2+1 ditranslasi oleh, persamaan parabola y=x^2-13x+40, persamaan parabola y=x^2+1 ditranslasikan oleh matriks, parabola y=x^2-3x-10, parabola y=-x^2+2x+1, parabola y=x^2-8x+12,




0 件のコメント:
コメントを投稿