The first portion of the file indicates progress of the calculation and some details about the symmetry of your system We can scroll ahead to the bottom to look at the 3N5=4 vibrational modes of carbon dioxide(2) The spacing between adjacent levels is not equal, it decreases with increasing quantum number;Now let's look at the output of our vibrational calculation!

Infrared Spectroscopy An Overview Sciencedirect Topics
3n-5 vibrational modes
3n-5 vibrational modes-Assigning Symmetries of Vibrational Modes C David Sherrill School of Chemistry and Biochemistry Georgia Institute of Technology June 00;Vibrational modes are what is left over For a linear molecule, we have 3N minus 5 vibrational modes If we have a nonlinear molecule, since we have three rotational modes in a nonlinear molecule, we have leftover 3N minus 6 vibrational modes Now, let's take a look at this a little bit more in detail Let's start with nitrogen Two atoms



Problem Set 5 Solutions
All you need is a change The terms "polar" and "nonpolar3N5 vibrational modes for linear molecules (limited number of molecules) A rule of Savannah bigger the molecule → more bands, so lots of information can be extracted about a molecule from its IR spectrum 12vibrational modes that have the same energy are degenerate This means that their bands overlapThe first portion of the file indicates progress of the calculation and some details about the symmetry of your system We can scroll ahead to the bottom to look at the 3N5=4 vibrational modes of carbon dioxide
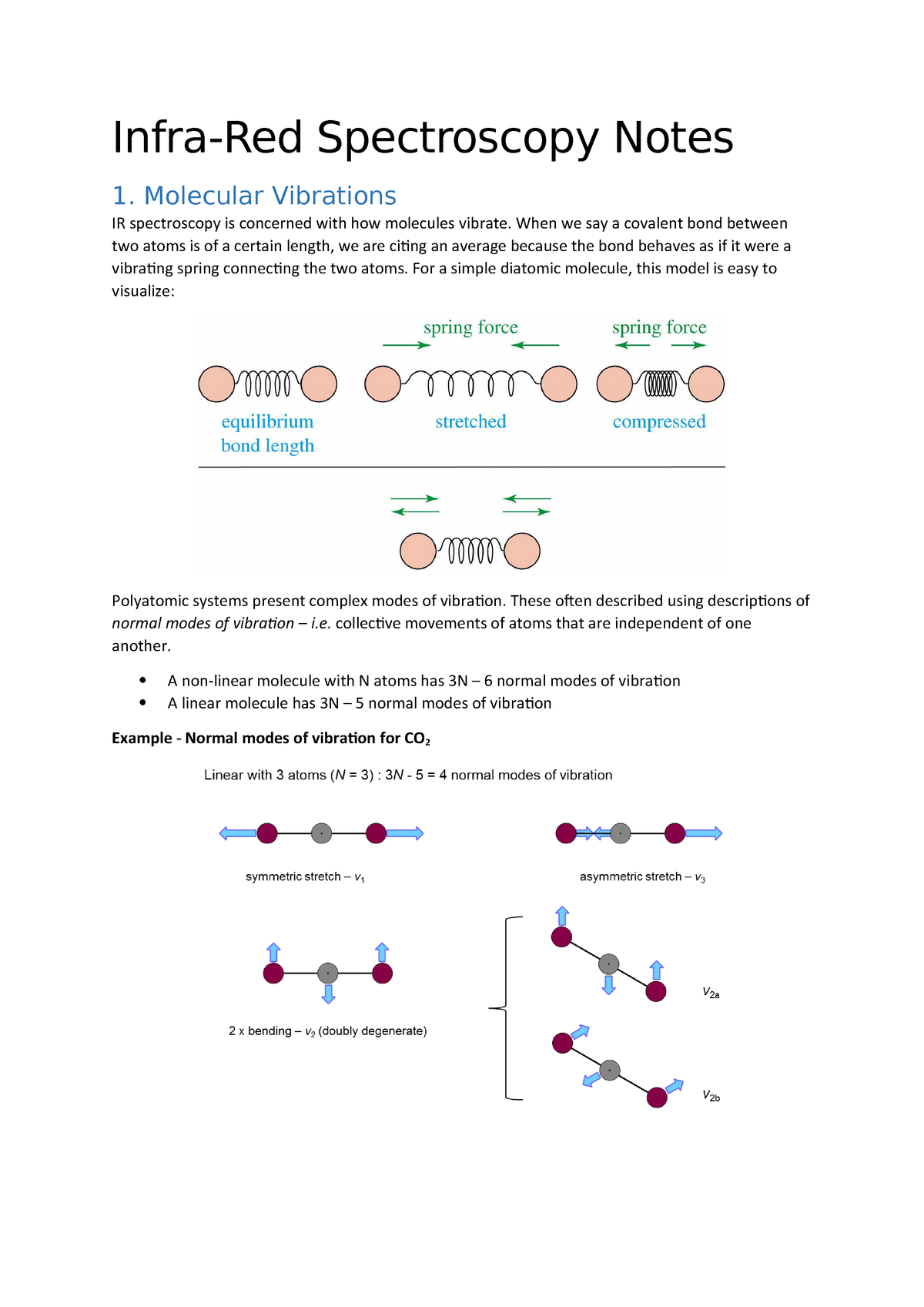
The degrees of vibrational modes for linear molecules can be calculated using the formula (1) 3 N − 5 The degrees of freedom for nonlinear molecules can be calculated using the formula (2) 3 N − 6 n is equal to the number of atoms within the molecule of interestKnown as a mode Linear molecules, such as CO 2, have 3N5 vibrational modes because 3 of all the modes result in a translation and 2 in a rotation ν (s) C=O IR inactive, Raman active 1285 cm1 2349 cm1 666 cm1 δ (s) O=C=O IR active, degenerated ν (as) C=O IR active, Raman activeVibrational Spectroscopy (IR, Raman) Vibrational spectroscopy In order to describe the 3N6 or 3N5 different possibilities how nonlinear and linear molecules containing N atoms can vibrate, the models of the harmonic and anharmonic oscillators are used These modes of vibration (normal modes) give rise to • absorption bands (IR)
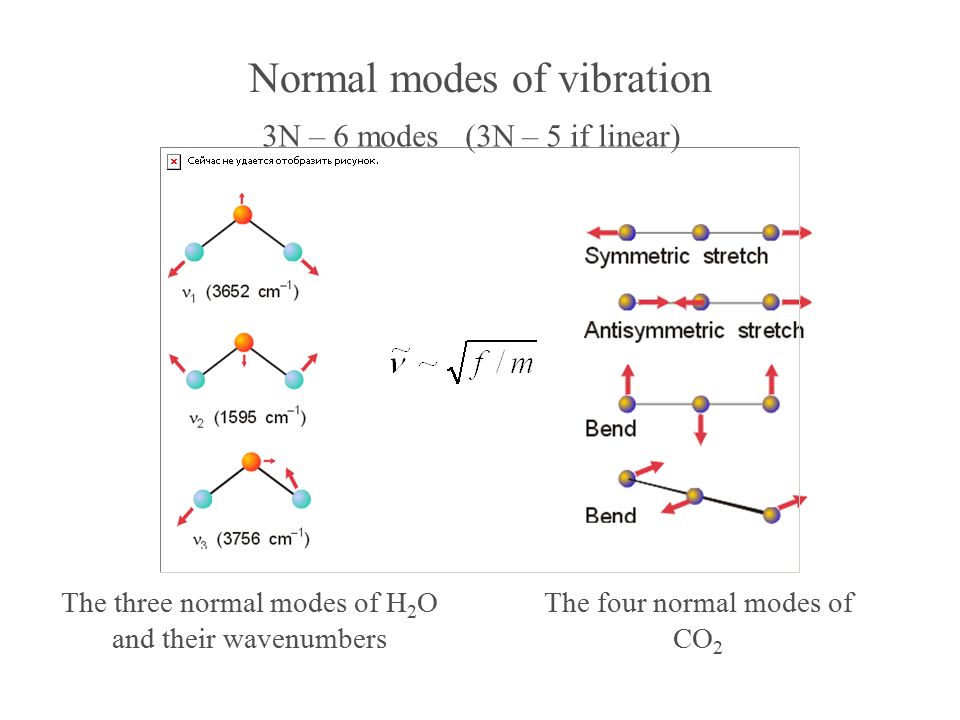
VibrationalRotational Spectroscopy VibrationalRotational Spectrum of Heteronuclear Diatomic Absorption of midinfrared light (~ cm1) • Molecules can change vibrational and rotational states • Typically at room temperature, only ground vibrational state populated but several rotational levels may be populatedThe realworld potential determines the vibrational properties, and they are different from those of an idealized harmonic oscillator (1) There is only a finite number of vibrational states (\(n=0,1,\dots,n_\mathrm{max}\));As carbon dioxide is a linear molecule of three atoms, we need the 3N 5 formula to determine how many vibrational modes it has Plugging in '3' gives us four vibrational modes Two of these modes are degenerate and correspond to different directions that are indistinguishable
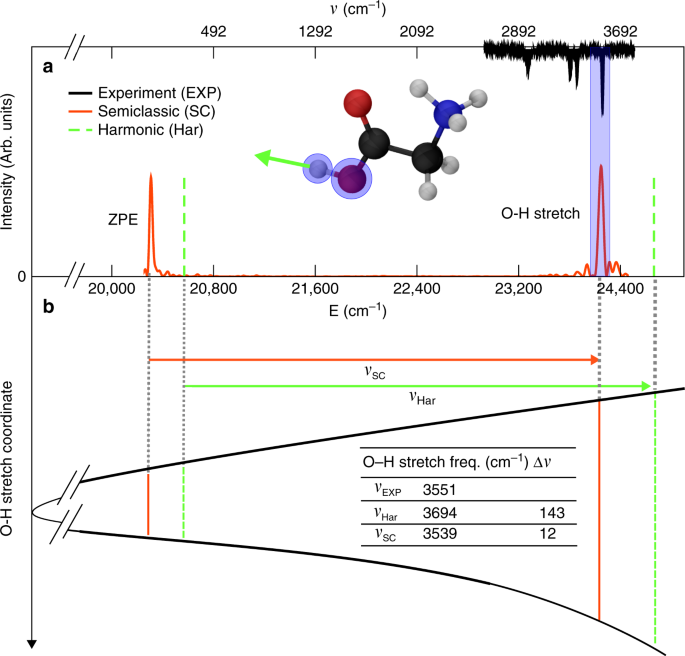


Anharmonic Quantum Nuclear Densities From Full Dimensional Vibrational Eigenfunctions With Application To Protonated Glycine Nature Communications



Vibrational Spectroscopy Of Linear Molecules Wikipedia
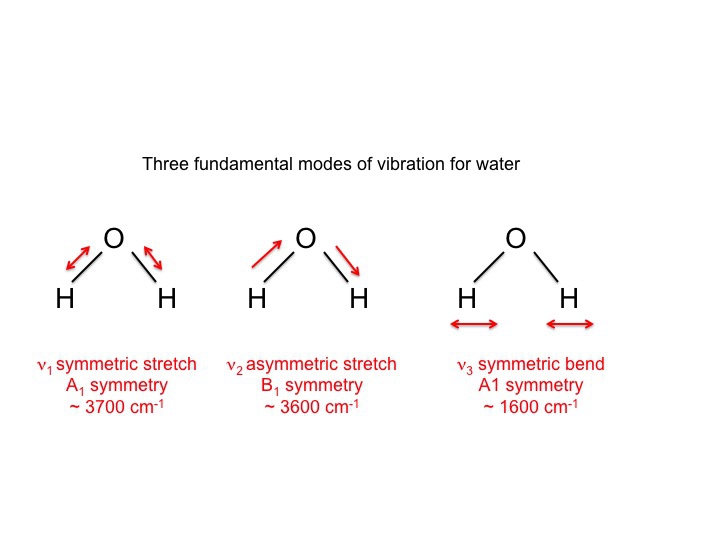
!1 symmetric stretch (ν = 1380 cm1) Three of these modes alter the dipole moment of !the molecule (both bends and the asym stretch);When subtracting the translational and rotational degrees of freedom, the degrees of vibrational modes is determined Number of degrees of vibrational freedom for nonlinear molecules 3N6 Number of degrees of vibrational freedom for linear molecules 3N5 Symmetry of vibrational modes3N5 = 3(3)5 = 4 The motion of the symmetrical stretch (ν 1) does not create a new dipole moment, so it is not observed in the IR spectrum Optical selection rule 2 a change in molecular dipole moment (∆μ/∆x) must occur with the vibrational motion of a mode Consider CO 2 (a linear molecule)



Solved 1 The Lab Manual States That The Number Of Vibra Chegg Com



Chemical Principles Lectures
Which is 3N6 (3N5 for a linear molecule) for a molecule with N nuclei For example, N 2 O is a linear triatomic molecule and has four normal modes of vibration (and only two of rotation) Associated with each normal mode is a vibrational frequency and a normal coordinate The vibrational frequency is easily calculated from nuclear masses, force2 has 3N5 = 4 vibrational modes!For linear molecules, there is one less rotational degree of freedom and the number of vibrational modes is therefore 3N – 5 Not all vibrational modes can be detected using Raman spectroscopy For a vibrational mode to be measured it must be 'Raman Active' which occurs when the molecular polarisability changes during the vibration



Chem Is Try October 10



Infrared Spectroscopy An Overview Sciencedirect Topics
If the molecule is linear, there are 3N – 5 modes of vibration Each atom may be displaced in any one of three directions (x, y, z), giving 3N possible displacements Three coordinates are required to specify the location of the centre of mass of the molecule (fixing the location of the molecule in space)These fundamental vibrations are referred to as "normal modes" Thus, a nonlinear molecule has 3N6 normal modes For water the number of normal modes is 3 (3 x 3 6 = 3) For linear molecules there are 3N5 normal modes For water, which of course has been intensively studied we know that the 3 vibrations are as followsMolecules with more than three atoms are even more complicated and have even more vibrations which are sometimes called "vibrational modes" Each new vibrational mode is basically a different combination of the six shown above The more atoms in the molecule the more ways they can be combined For most molecules with N atoms the number of possible vibrations for that molecule is 3N 6 while linear molecules, or molecules with there atoms in a straight line, have 3N5 vibrational modes


Infrared Spectroscopy



How Do Co2 Molecules Vibrate Quora
A molecule can vibrate in many ways, and each way is called a vibrational mode For molecules with N atoms in them, linear molecules have 3N – 5 degrees of vibrational modes, whereas nonlinear molecules have 3N – 6 degrees of vibrational modes (also called vibrational degrees of freedom)!2 "degenerate" bends (ν = 667 cm1)!Bookmark this question Show activity on this post I'm facing difficulty understanding how vibrational energy modes contribute to a molecule's average energy (or heat capacity) What I know is For a polyatomic nonlinear molecule, there are 3 N − 6 normal modes of vibration ( 3 N − 5 for linear molecule) Also, in a onedimensional harmonic oscillator, ( 1 / 2) k T contribution to energy comes from potential energy, and ( 1 / 2) k T from kinetic energy



Rubric1 Reflection3



Treating Linear Molecule Hcch In Calculations Of Rotation Vibration Spectra The Journal Of Chemical Physics Vol 149 No 1
The number of vibrational degrees of freedom is showing by Z=3N‐6 for nonlinear molecules and Z = 3N‐5 for linear molecules A linear three atomic molecule like CO 2 has 4, a nonlinear three atomic molecule like H 2 O has 3, NH 3 ,NH 4!1 asymmetric stretch (ν = 2349 cm1)!For molecules with N number of atoms, linear molecules have 3N – 5 degrees of vibrational modes, whereas nonlinear molecules have 3N – 6 degrees of vibrational modes (also called vibrational degrees of freedom) As an example H 2 O, a nonlinear molecule, will have 3 × 3 – 6 = 3 degrees of vibrational freedom, or modes


Raman Spectroscopy Chapter 6 Remote Compositional Analysis



Decoding Chemical Information From Vibrational Spectroscopy Data Local Vibrational Mode Theory Kraka Wires Computational Molecular Science Wiley Online Library
As carbon dioxide is a linear molecule of three atoms, we need the 3N 5 formula to determine how many vibrational modes it has Plugging in '3' gives us four vibrational modes Two of these modes are degenerate and correspond to different dire!one does not (the sym stretch) This means that CO 2 can absorb and radiate IR light atNow let's look at the output of our vibrational calculation!


Degrees Of Freedom Of A Linear Triatomic Molecule Physics Stack Exchange



Degrees Of Freedom Six Of A Diatomic Molecule Only One Vibration Download Scientific Diagram
If the molecule is linear, there are 3N – 5 modes of vibration Each atom may be displaced in any one of three directions ( x , y, z ), giving 3N possible displacements Three coordinates are required to specify the location of the centre of mass of the molecule (fixing the location of the molecule in space)A particular molecule with N atoms has 3N6 vibrational modes if it is nonlinear, and 3N5 vibrational modes if it is linear A molecule can absorb a photon of IR light and increase the vibrational energy of one of its vibrational modes However, not all vibrational modes can increase in energy by absorbing a photon in the IR region For a molecular vibrational mode to be IR active, the dipole moment of the molecule must change during the vibrational modeThe number of molecular vibrational modes equals 3n6 (3n5 for linear molecules), where n is the number of atoms An ir active band will be observed if a vibration results in a change of the dipole moment The initial dipole moment in the molecule's equilibrium geometry can be zero;



How It Looks From Here Molecules And Radiation Ii Molecular Vibration Rotation And Translation



Ir Spectroscopy Presented By Dipsankar
These fundamental vibrations are referred to as "normal modes" Thus, a nonlinear molecule has 3N6 normal modes For water the number of normal modes is 3 (3 x 3 6 = 3) For linear molecules there are 3N5 normal modes For water, which of course has been intensively studied we know that the 3 vibrations are as followsVibrational These are any other types of movement not assigned to rotational or translational movement and thus there are 3N – 6 degrees of vibrational freedom for a nonlinear molecule and 3N – 5 for a linear molecule These vibrations include bending, stretching, wagging and many other aptly named internal movements of a moleculeVibrational These are any other types of movement not assigned to rotational or translational movement and thus there are 3N – 6 degrees of vibrational freedom for a nonlinear molecule and 3N – 5 for a linear molecule These vibrations include bending, stretching, wagging and many other aptly named internal movements of a molecule


Molecular Vibrations Explained Animated Guides Specac



Problem Set 5 Solutions
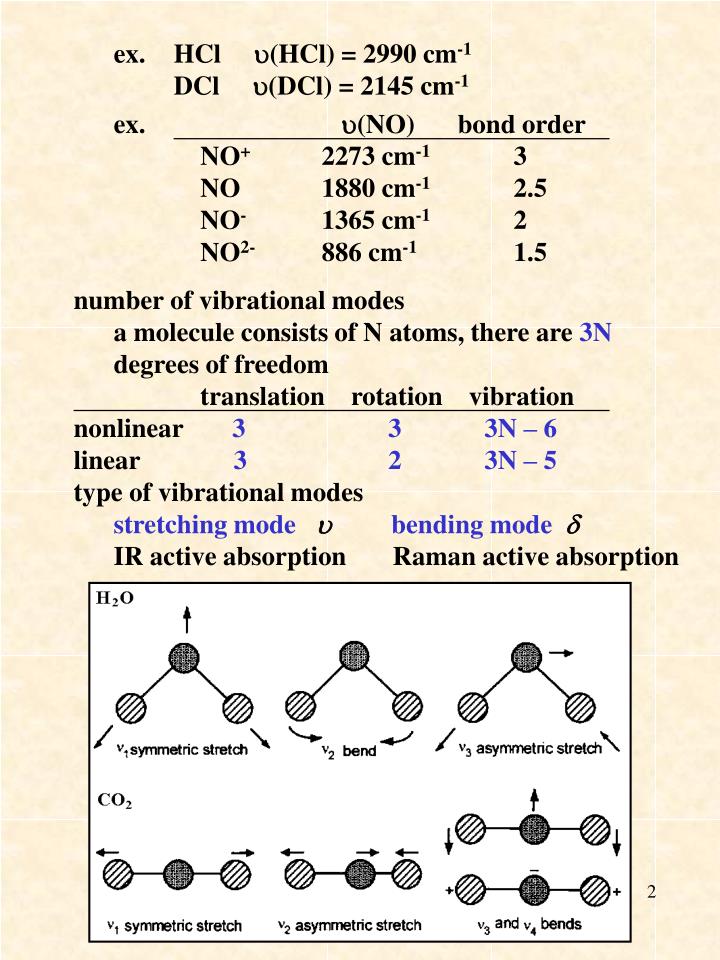
A diatomic molecule has one molecular vibration mode, where the two atoms oscillate back and forth with the chemical bond between them acting as a spring A molecule with N atoms has more complicated modes of molecular vibration, with 3N − 5 vibrational modes for a linear molecule and 3N − 6 modes for a nonlinear moleculeNormal mode is treated as a simple harmonic oscillator Symmetric stretch Asymmetric stretch Bend Bend Figure 1 Normal Modes for a linear triatomic molecule In the last bending vibration the motion of the atoms is inandout of the plane of the paper In general linear molecules have 3N5 normal modes, where N is the number of atomsThe number of vibrational normal modes can be determined for any molecule from the formula given above For a diatomic molecule, N = 2 so the number of modes is 3 × 2 − 5 = 1 For a triatomic linear molecule (CO 2), it is 3 × 3 − 5 = 4 and triatomic nonlinear molecule (H 2 O), it is 3 × 3 − 6 = 3 and so on Example 1 Water


Mcq On Ir Spectroscopy Page 1


Ppt Vibrational Infrared Spectroscopy Powerpoint Presentation Free Download Id
A linear molecule possesses 3n 5 vibrational modes (3 translations, 2 rotations) A nonlinear molecule possesses 3n 6 vibrational modes (3 translations, 3 rotations) Like the diatomic case, each normal mode of vibration has a characteristic frequency and can assume a series of quantized energiesRevised July 10 1 Introduction Group theory is a very powerful tool in quantum chemistry By analyzing the symmetry propertiesAccepted 7 May 1987) Frequencies and intensities are calculated by ab initio methods for all vibrational modes of the The normal modes of vibration are asymmetric


Solved 1 Use The Rule Of 3n 6 Nonlinear Molecule Or 3n Chegg Com



Solved 1 Use The Rule Of 3n 6 Nonlinear Molecule Or 3n Chegg Com
For linear molecules, there is one less rotational degree of freedom and the number of vibrational modes is therefore 3N – 5 Not all vibrational modes can be detected using Raman spectroscopy For a vibrational mode to be measured it must be 'Raman Active' which occurs when the molecular polarisability changes during the vibrationHttp//enwikipediaorg/wiki/Molecular_vibration For a molecule of N atoms there are 3N6 normal modes (nonlinear) or 3N5 (linear)As a result, linear molecules have 3N 5 degrees of freedom Normal Modes 161 3/7 O HH O HH O HH symmetric asymmetric bend stretch stretch H Infrared Inactive Modes 161 7/7 In order for a vibrational transition to be infrared active, the motion along the normal coordinate has to change the molecular dipole moment



Ir Spectroscopy P K Mani kv West Bengal India



Number Of Vibrational Modes
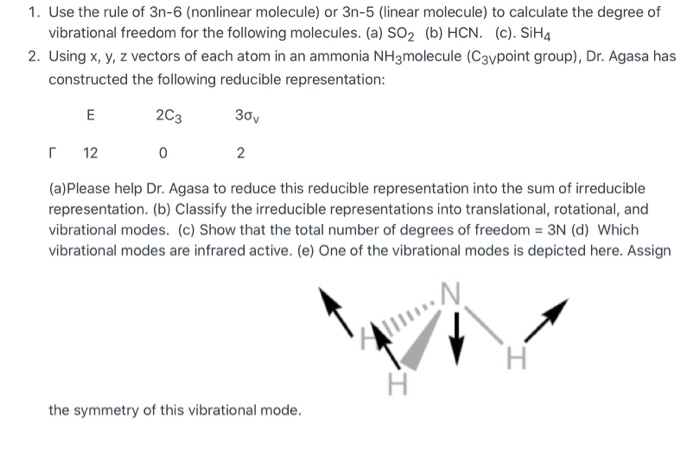
Are separated out, leaving 3N 6 or 3N 5 modes for vibrational analysis The rest of this section describes how the Sayvetz conditions are used to generate the translation and rotation vectors The three vectors (D 1, D 2, D 3) of length 3Ncorresponding to translation are trivial to generate in cartesian coordinates They are just pThe number of vibrational modes of a molecule is determined by the equation 3N6 for a nonlinear molecule and 3N5 for a linear molecule (N is number of atoms in the molecule) For the following, draw the Lewis structure and predict the number of vibrational modes expected a CC14 b CO2 c CH3COOHBasics of vibrational spectroscopy 11 Molecular vibrations and normal modes 12 Normal mode analysis 3N6 and 3N5 for nonlinear and linear molecules, respectively normal modes are characterised by frequencies (given in cm1)


Correlation Between Molecular Acidity Pk A And Vibrational Spectroscopy Springerlink


Infrared Spectra Image And Video Exchange Forumimage And Video Exchange Forum
What is left is vibrational 3N – 5 for linear (5 = 3 for translational 2 for rotational) 3N – 6 for nonlinear (6 = 3 for translational 3 for rotational)For water the number of normal modes is 3 (3 x 3 6 = 3) For linear molecules there are 3N5 normal modes For water, which of course has been intensively studied we know that the 3 vibrations are as follows The symbols used to describe these modes (A 1, B 1) are the same Mulliken symbols that we encountered in our discussion of character tables In other words, the vibrations, which are molecular properties, can described by symmetry species or irreducible representationsA particular molecule with N atoms has 3N6 vibrational modes if it is nonlinear, and 3N5 vibrational modes if it is linear A molecule can absorb a photon of IR light and increase the vibrational energy of one of its vibrational modes However, not all vibrational modes can increase in energy by absorbing a photon in the IR region For a


Solved 2 Acetylene C2h2 Is A Symmetrical Linear Molecule With A Total Of 7 Normal Modes Descriptions Of Some Of The Vibrational Modes Are Given Course Hero



Ppt Rotational And Vibrational Spectroscopy Powerpoint Presentation Free Download Id
The remaining 3N6 degrees of freedom (3N5 if linear) describe vibrations Symmetry species of translations, rotations, and vibrations can be determined by considering the normal modes of vibration It is informative to consider the symmetries of the vibrationalDegrees of Freedom and Vibrational Modes 1 Every atom in a molecule can move in three possible directions relative to a Cartesian coordinate, so for a molecule of n atoms there are 3 n degrees of freedom 2 For a linear molecule, there are 3 translations and 2 rotations of the system, so the number of normal modes is 3 n – 5 3Complexes of NH3 and PH3 with HF Ingrid J Kurnig,a) M M SzczE;Jsniak, and Steve Scheinerb)C) Department o/Chemistry and Biochemistry, Southern Illinois University, Carbondale, Illinois (Received 13 February 1987;



Problem Set 5 Solutions



Vibrational Modes Of Co 2 Image Credit Kristin Spear Nasa Glenn Download Scientific Diagram
• The vibrational partition function is treated as follows Note for a linear triatomic the 3N5 rule states there are four vibrational modes in the partition function corresponding to symmetric and asymmetric stretches and two equivalent bending modesVibrational modes Example of a linear molecule N atoms in a molecule have 3N degrees of freedom which constitute translations, rotations, and vibrations Find the number of normal (vibrational) modes or degrees of freedom using the equation 3n 5 = 3(3) 5 = 4 4A molecular vibration is a periodic motion of the atoms of a molecule relative to each other, such that the center of mass of the molecule remains unchanged The typical vibrational frequencies range from less than 10 13 Hz to approximately 10 14 Hz, corresponding to wavenumbers of approximately 300 to 3000 cm −1 Vibrations of polyatomic molecules are described in terms of normal modes


Ir Notes Summary On All Of Ir Infra Red Spectroscopy Notes Molecular Studocu


Normal Modes Of Vibration Ch 431 Inorganic Chemistry
Molecular Motions Vibrations of Molecules Model approximates molecules to atoms joined by springs A vibration (one type of –a normal mode of vibration) of a CH2moiety would look like;A linear $\ce{AB2}$ molecule will have $(3n5) = 4$ vibrational modes, but because it is linear 2 of the modes are degenerate $\ce{CO2}$ is an example of a linear $\ce{AB2}$ molecule, look at the following diagram showing the 4 vibrations for $\ce{CO2}$ and notice that the bending vibration ($v_2$) is degenerate



How To Calculate Symmetries Of Vibrational Normal Modes Part 1 Example Water H2o Youtube


Infrared Spectroscopy Ir Vibrational Spectroscopy Is An Energy Sensitive Method And Is Used To Characterize Compounds In Terms Of The Strengths And Number Ppt Download


Vibrational Properties Of Molecules Hjkgrp Mit Edu


Symmetry Of Gold Neutral Clusters Au3 And Normal Modes Of Vibrations By Using The Numerical Finite Difference Method With Density Functional Tight Binding Dftb Approach Insight Medical Publishing



Vibrational Modes Infrared Spectroscopy Coursera



Molecular Symmetry 1 Pdf Free Download



Theme 2 Lecture 2 Pptx Molar Internal Energy For A Linear Triatomic Gas X Y Z Directions X Y Directions See Next Slide There Is No Moment Of Inertia Course Hero



Introduction To Vibrations Chemistry Libretexts


A Seminar On Infrared Spectroscopy Ppt Download
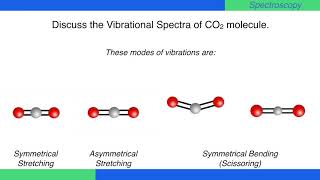


Discuss The Vibrational Spectra Of Co2 Molecule Spectroscopy Physicalchemistry Youtube



Chapter 7 Symmetry And Spectroscopy Molecular Vibrations P Pdf Document



Rubric1 Reflection3
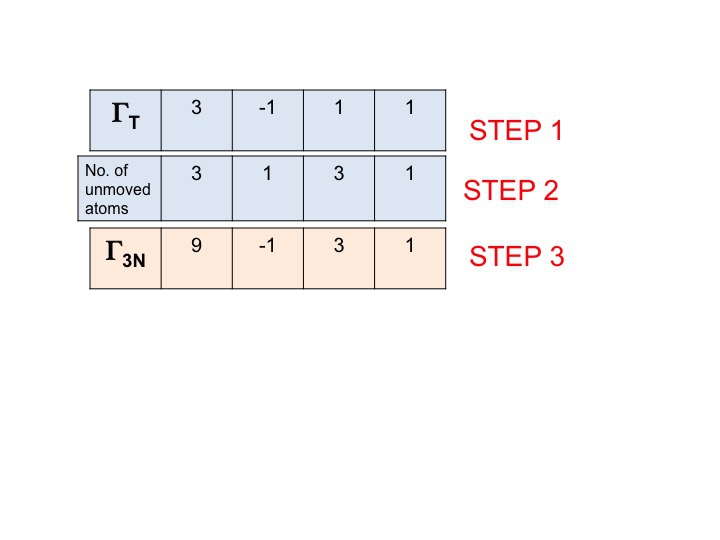


Normal Modes Of Vibration Ch 431 Inorganic Chemistry


Group Theory And Vibrational Spectroscopy



8 Answer The Following Questions About Co2 A What Is The Theoretical Number Vibrational Modes Of Homeworklib


Infrared Spectroscopy



On The Basis Of Raman Spectroscopy Explain The Structure Of Co2 Raman Spectra Physical Chem Youtube



How Many Vibrational Modes Are There In The Co 2 And H2o And Draw Brainly In



Vibrational Spectroscopy Powerpoint Slides



Hydrogen Cyanide Hcn Is A Linear Polyatomic Molecule I Calculate The Number Of Normal Modes Of Homeworklib


Exam 2



Vibrational Spectroscopy Powerpoint Slides


Group Theory And Vibrational Spectroscopy
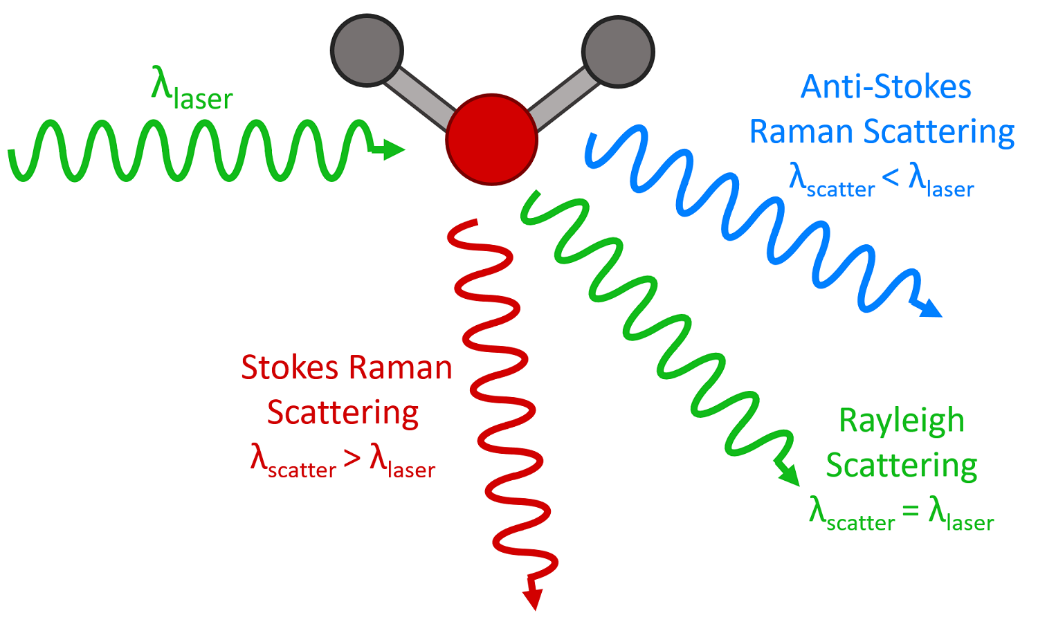


What Is Raman Spectroscopy Raman Spectroscopy Principle



Solved Question 1 The Number Of Vibrational Modes For A Chegg Com


Molecular Motion Chemistry Topics



Generalchem Ls 14 Pdf Raman Spectroscopy Normal Mode
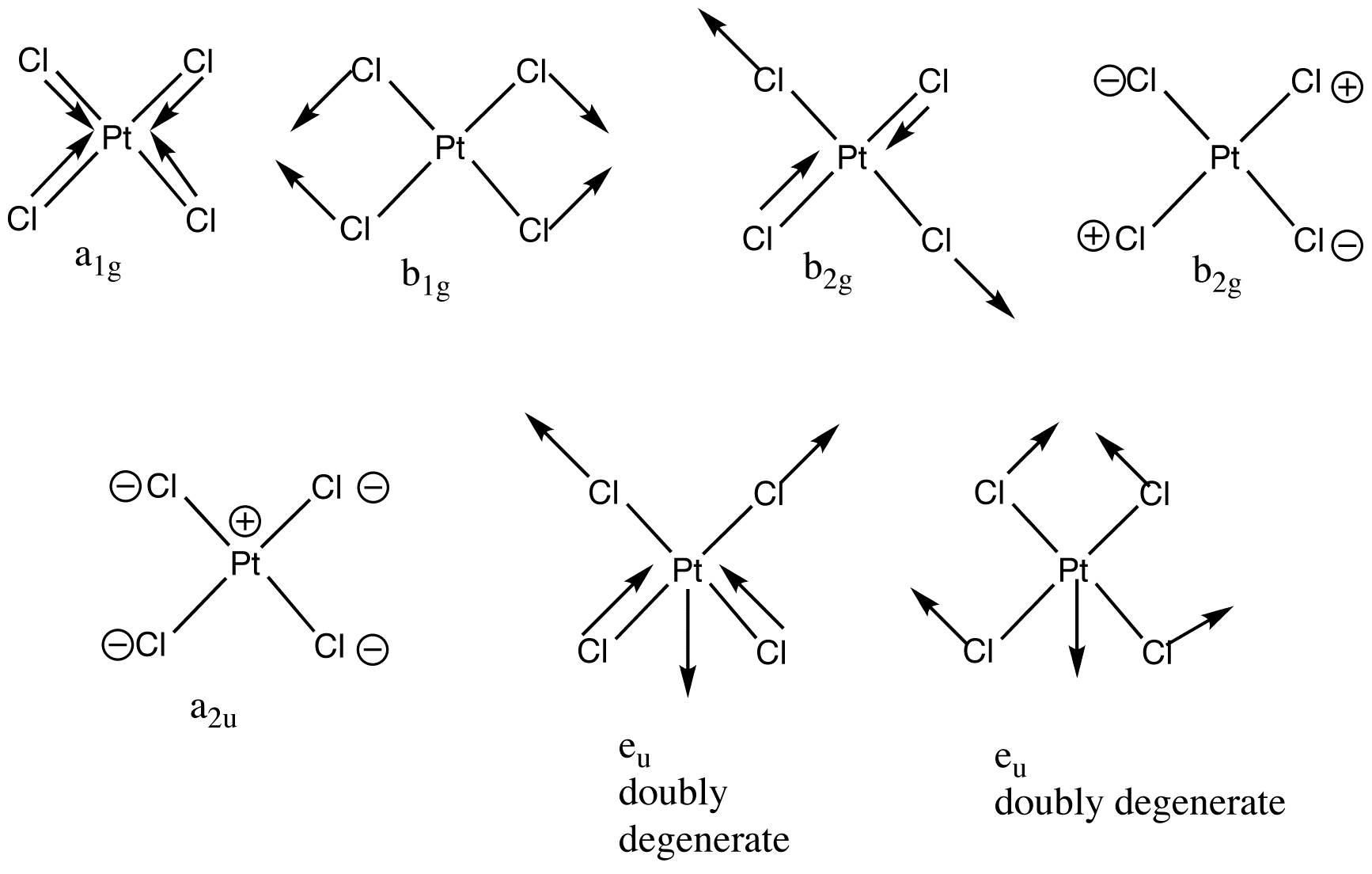


Normal Modes Chemistry Libretexts


Vibrational Frequencies Of Water Molecule
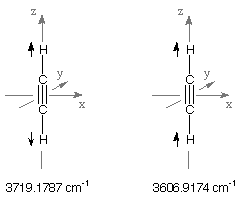


Vibrational Frequencies



Symmetry And Molecular Modes Of Vibrations Nonlinear Translation Rotation Molecule 3n 6 Linear Molecule 3n 5 Vibrational Spectroscopy Ir Ir Pdf Document
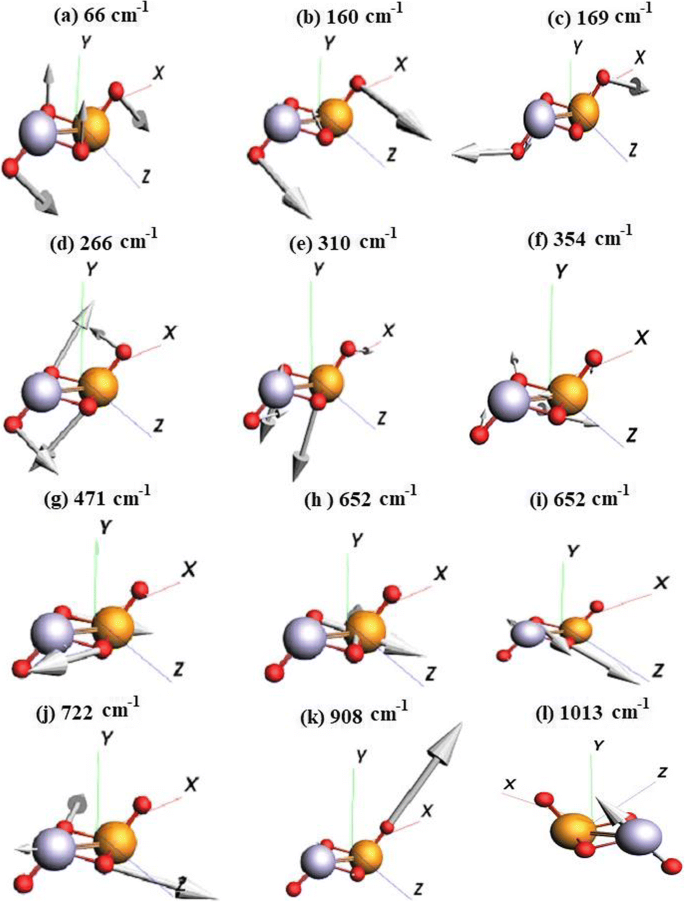


First Principles Investigations Of Vibrational Properties Of Titania And Zirconia Clusters Springerlink
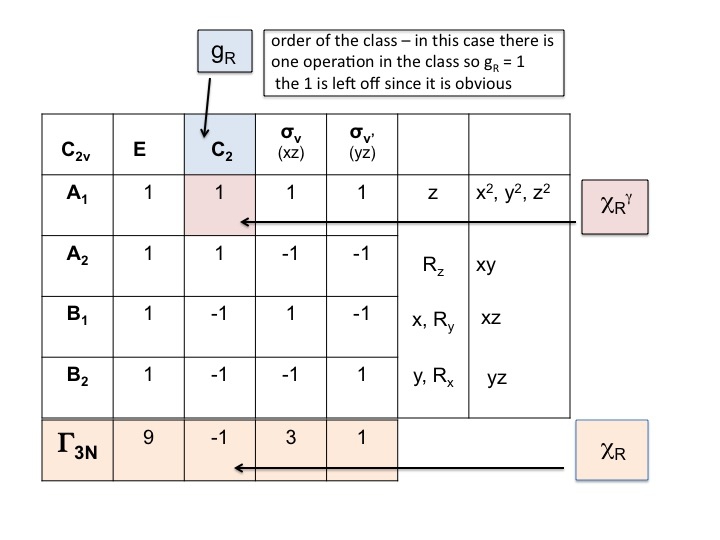


Normal Modes Of Vibration Ch 431 Inorganic Chemistry



Ppt Dong Powerpoint Presentation Free Download Id



Experiment 9 Rotational Vibrational Spectroscopy Introduction



The Vibrational Spectrum Of A Polyatomic Molecule Chemistry


Degrees Of Freedom In A Molecule Physics Forums



Infrared Absorption Spectroscopy Ppt Download



Intro To Molecular Vibrations And Ir Spectroscopy



Molecular Vibration Wikipedia
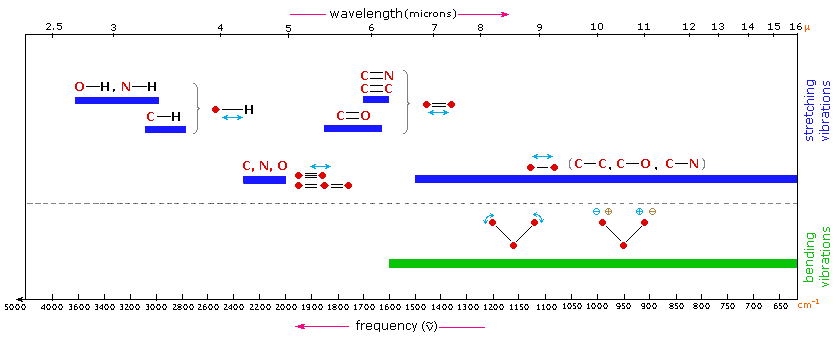


Infrared Spectroscopy



Molecular Vibration An Overview Sciencedirect Topics


Assigning Vibrational Frequencies Anorganische Chemie Universitat Rostock



0 件のコメント:
コメントを投稿